July 2021
•
August 2021
•
September 2021
Best of August 2021
If the Facebook link isnt available, then the page or post is likely deleted.
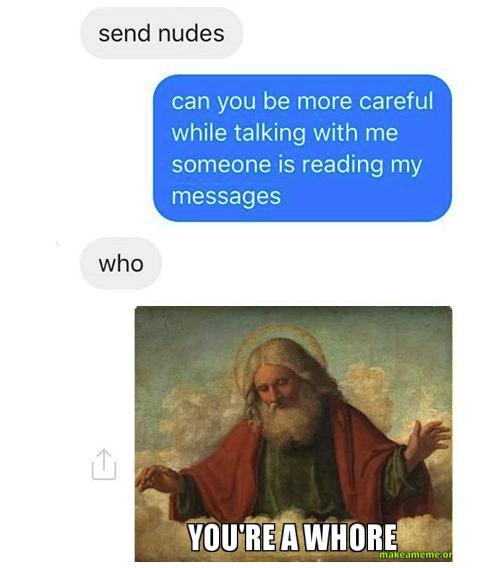
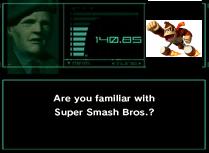
#1:
2387 reacts
(FB)
19 August 2021
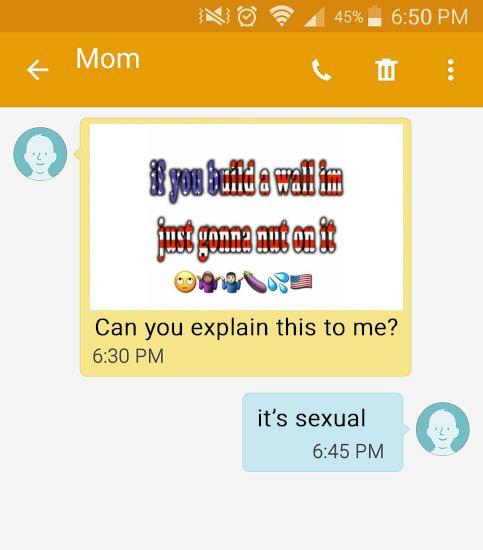
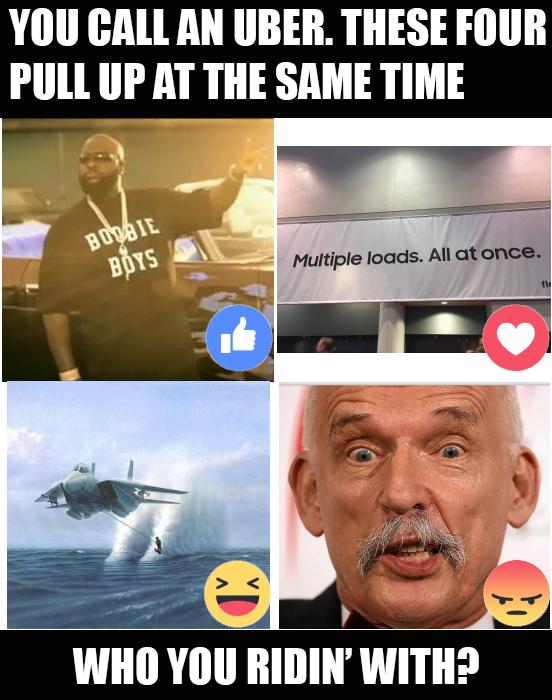
#2:
1317 reacts
(FB)
26 August 2021
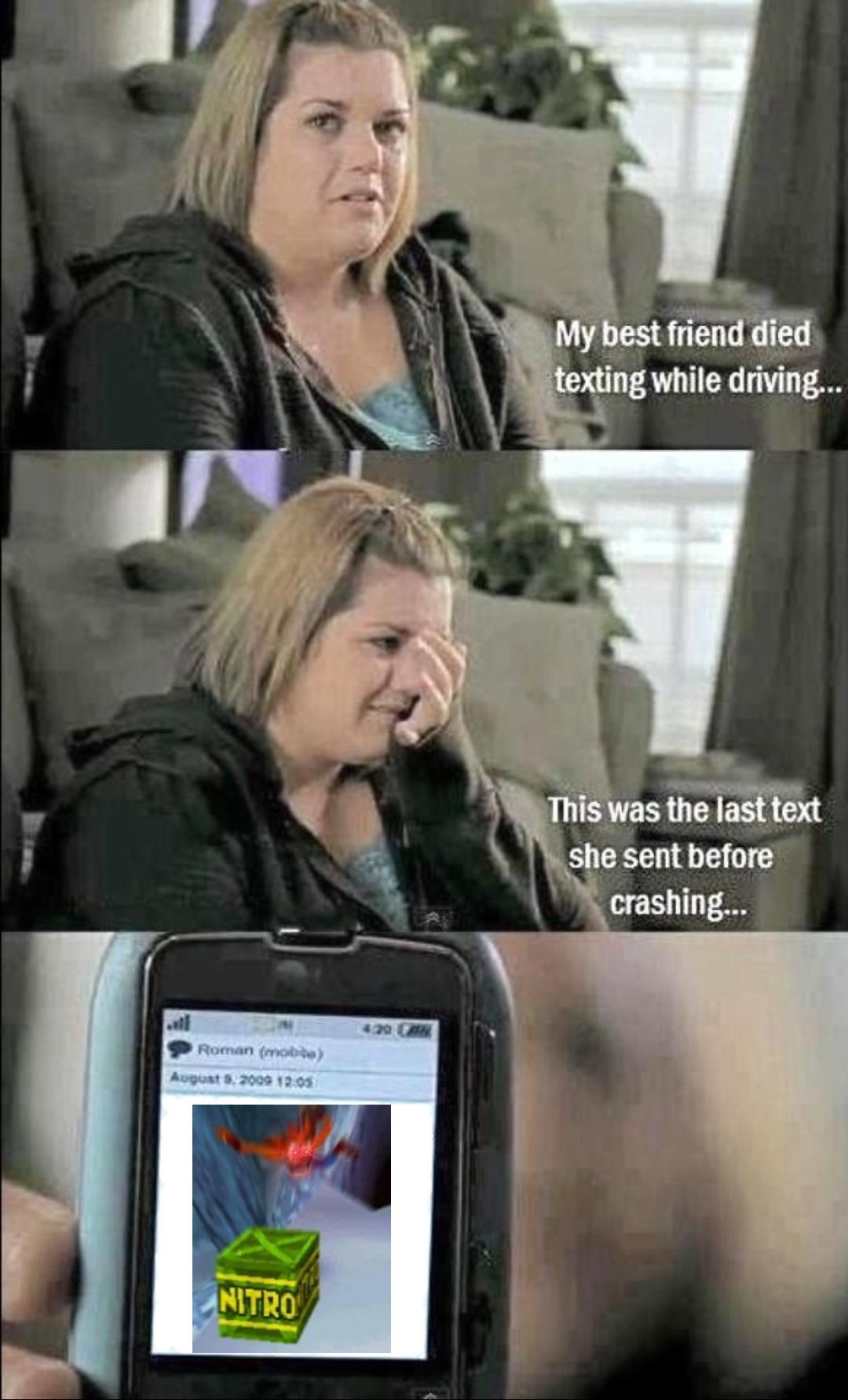
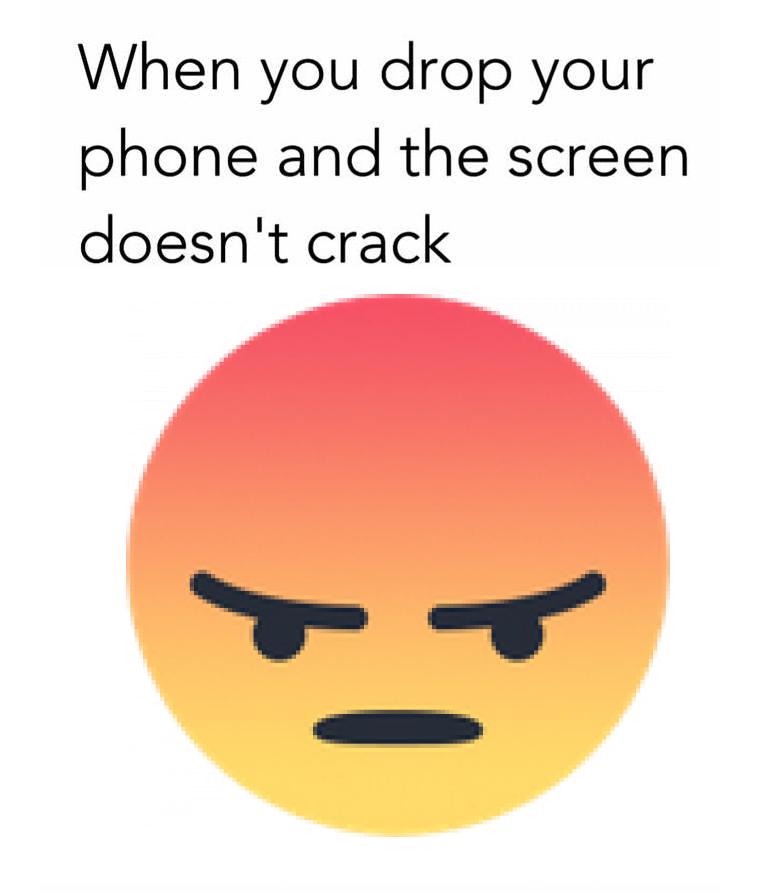
#3:
1277 reacts
(FB)
24 August 2021
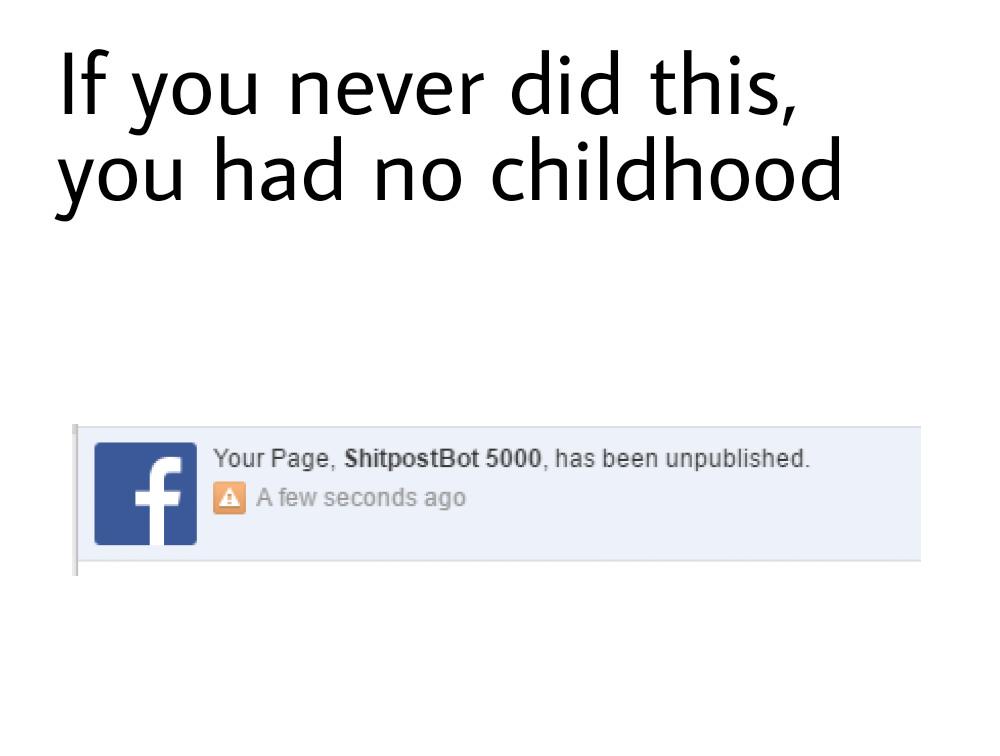
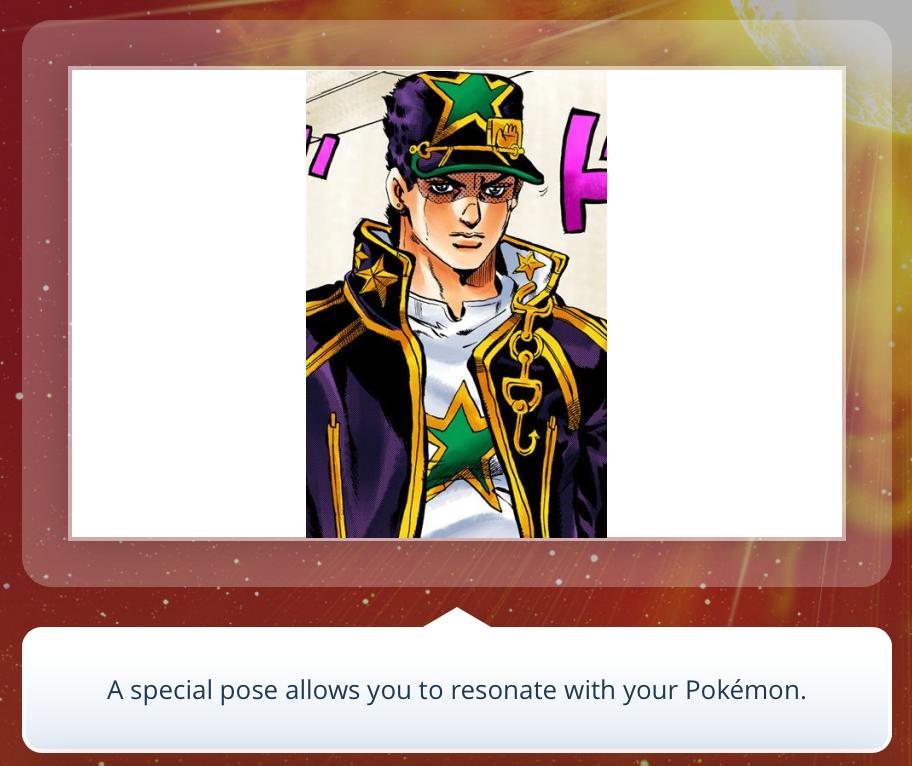
#4:
672 reacts
(FB)
24 August 2021
#5:
554 reacts
(FB)
26 August 2021
#6:
504 reacts
(FB)
24 August 2021
#7:
491 reacts
(FB)
19 August 2021
#8:
488 reacts
(FB)
25 August 2021
#9:
475 reacts
(FB)
22 August 2021
#10:
461 reacts
(FB)
23 August 2021
#11:
382 reacts
(FB)
19 August 2021
#12:
374 reacts
(FB)
22 August 2021
#13:
373 reacts
(FB)
23 August 2021
#14:
317 reacts
(FB)
24 August 2021
#15:
306 reacts
(FB)
22 August 2021
#16:
299 reacts
(FB)
23 August 2021
#17:
286 reacts
(FB)
22 August 2021
#18:
281 reacts
(FB)
23 August 2021
#19:
278 reacts
(FB)
19 August 2021
#20:
264 reacts
(FB)
24 August 2021
#21:
256 reacts
(FB)
26 August 2021
#22:
241 reacts
(FB)
26 August 2021
#23:
238 reacts
(FB)
19 August 2021
#24:
229 reacts
(FB)
19 August 2021
#25:
226 reacts
(FB)
19 August 2021
#26:
226 reacts
(FB)
25 August 2021
#27:
218 reacts
(FB)
20 August 2021
#28:
216 reacts
(FB)
20 August 2021
#29:
214 reacts
(FB)
22 August 2021
#30:
204 reacts
(FB)
23 August 2021
#31:
202 reacts
(FB)
22 August 2021
#32:
196 reacts
(FB)
23 August 2021
#33:
193 reacts
(FB)
19 August 2021
#34:
192 reacts
(FB)
25 August 2021
#35:
186 reacts
(FB)
22 August 2021
#36:
186 reacts
(FB)
24 August 2021
#37:
185 reacts
(FB)
19 August 2021
#38:
184 reacts
(FB)
24 August 2021
#39:
179 reacts
(FB)
25 August 2021
#40:
178 reacts
(FB)
24 August 2021
#41:
175 reacts
(FB)
25 August 2021
#42:
174 reacts
(FB)
19 August 2021
#43:
170 reacts
(FB)
24 August 2021
#44:
164 reacts
(FB)
25 August 2021
#45:
162 reacts
(FB)
24 August 2021
#46:
161 reacts
(FB)
22 August 2021
#47:
160 reacts
(FB)
19 August 2021
#48:
160 reacts
(FB)
22 August 2021
#49:
159 reacts
(FB)
23 August 2021
#50:
154 reacts
(FB)
24 August 2021
Privacy Policy